(C) 2013 Hazel R. Parry. This is an open access article distributed under the terms of the Creative Commons Attribution License 3.0 (CC-BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
For reference, use of the paginated PDF or printed version of this article is recommended.
Citation: Parry HR, Sadler RJ, Kriticos DJ (2013) Practical guidelines for modelling post-entry spread in invasion ecology. In: Kriticos DJ, Venette RC (Eds) Advancing risk assessment models to address climate change, economics and uncertainty. NeoBiota 18: 41–66. doi: 10.3897/neobiota.18.4305
In this article we review a variety of methods to enable understanding and modelling the spread of a pest or pathogen post-entry. Building upon our experience of multidisciplinary research in this area, we propose practical guidelines and a framework for model development, to help with the application of mathematical modelling in the field of invasion ecology for post-entry spread. We evaluate the pros and cons of a range of methods, including references to examples of the methods in practice. We also show how issues of data deficiency and uncertainty can be addressed. The aim is to provide guidance to the reader on the most suitable elements to include in a model of post-entry dispersal in a risk assessment, under differing circumstances. We identify both the strengths and weaknesses of different methods and their application as part of a holistic, multidisciplinary approach to biosecurity research.
Biosecurity, Dispersal, Migration, Modelling, Post-entry spread
Invasive species can have enormous economic and ecological impacts (
This article focuses on this ‘post-entry spread’ stage of the invasion process, specifically understanding dispersal processes and modelling the spread and establishment potential of a pest or pathogen once it has arrived into a region. We differentiate this from the population dynamics and dispersal of native species, as post-entry pest spread of non-native species has particular features that add to the modelling challenge. These include the requirement for rapid response, data paucity and high levels of uncertainty.
Whilst the majority of pest and pathogen entry today is largely due to anthropogenic pathways (
When integrated with field-based research and surveillance, dispersal models can help inform pest and pathogen outbreak management about a range of processes, such as the rate of spread of a pest (
With such diversity of pathways, scales and complexity of dispersal processes for post-entry spread, and with such a wide range of possible applications, there is a parallel diversity of modelling methods. We aim to give an overview here to help guide modellers to select appropriate methods.
Models of pest and pathogen spread post-entry largely occupy one of two categories of model: analytical methods (
To explore the long distance connectivity of populations, network models and metapopulation models have also been applied to invasion ecology in recent times (
Mechanistic, process-based simulationmodels are a more recent development for modelling spread post-entry (
It is also possible and can be advantageous for a dispersal model to contain both analytical and mechanistic components (e.g.
Multiple dispersal vectors add extra layers of complexity (
In addition, species niche models can inform post-entry spread in multiple ways. Firstly, they can inform the total area that can potentially be invaded. This information can define the spatial bounds of the spread modelling, i.e., the model ‘universe’, for both simulation and analytical spread models. Alternatively, a niche model can be used to differentiate between different components of a heterogeneous landscape over which a species may spread, and this can be used by spatially-explicit dynamic dispersal models (e.g.,
When considering how best to apply these models, understanding the ecology and landscape factors relevant to the population dynamic and dispersal of a pest or pathogen species is critical. Often, not enough consideration is given to an organism’s ecology and behaviour prior to developing a dispersal model, where population dynamics models are commonly separated from dispersal simulation. However, biological processes operating at different spatial and temporal scales are key drivers in the dispersal process, and ideally should be taken into account explicitly.
In selecting a model, there are also important characteristics to consider, such as the sensitivity of the model (the proportion of known spatio-temporal dispersal events modelled correctly) versus the specificity of the model (the proportion of unoccupied sites that are modelled correctly) (
The rate of spread of a pest or pathogen can affect the present value of its future economic and ecological impacts, taking into account the economic discount rate; all else being equal, a slower-spreading pest/pathogen is thought to have less potential future impact than a faster-spreading one. However, for terrestrial plants in particular, there may be a deceptive time lag between the arrival of the pest and the point at which the rate of spread begins to accelerate (
The International Standards for Phytosanitary Measures (
- suitability of the natural and/or managed environment for natural spread of the pest,
- movement with commodities or conveyances,
- intended use of the commodity,
- potential vectors of the pest in the outbreak area,
- potential natural enemies of the pest in the outbreak area.
In this regard, we seek to estimate the potential extent of the endangered area, as well as the likely rate at which that area might become occupied by the organism. In the early stages of response it is important to assess the factors above as rapidly as possible, along with the route of introduction, the mechanisms of subsequent movement and the shape of the natural dispersal kernel. Some factors will be easier to assess than others. While the potential extent can be estimated using niche modelling methods based on the organism’s overseas distribution and where available knowledge of its ecology, simulating the organism’s rate of spread relies on estimated spread rates, of which our knowledge is often poor. For example, use of Ripley’s K-function or an O-ring analysis with available data (
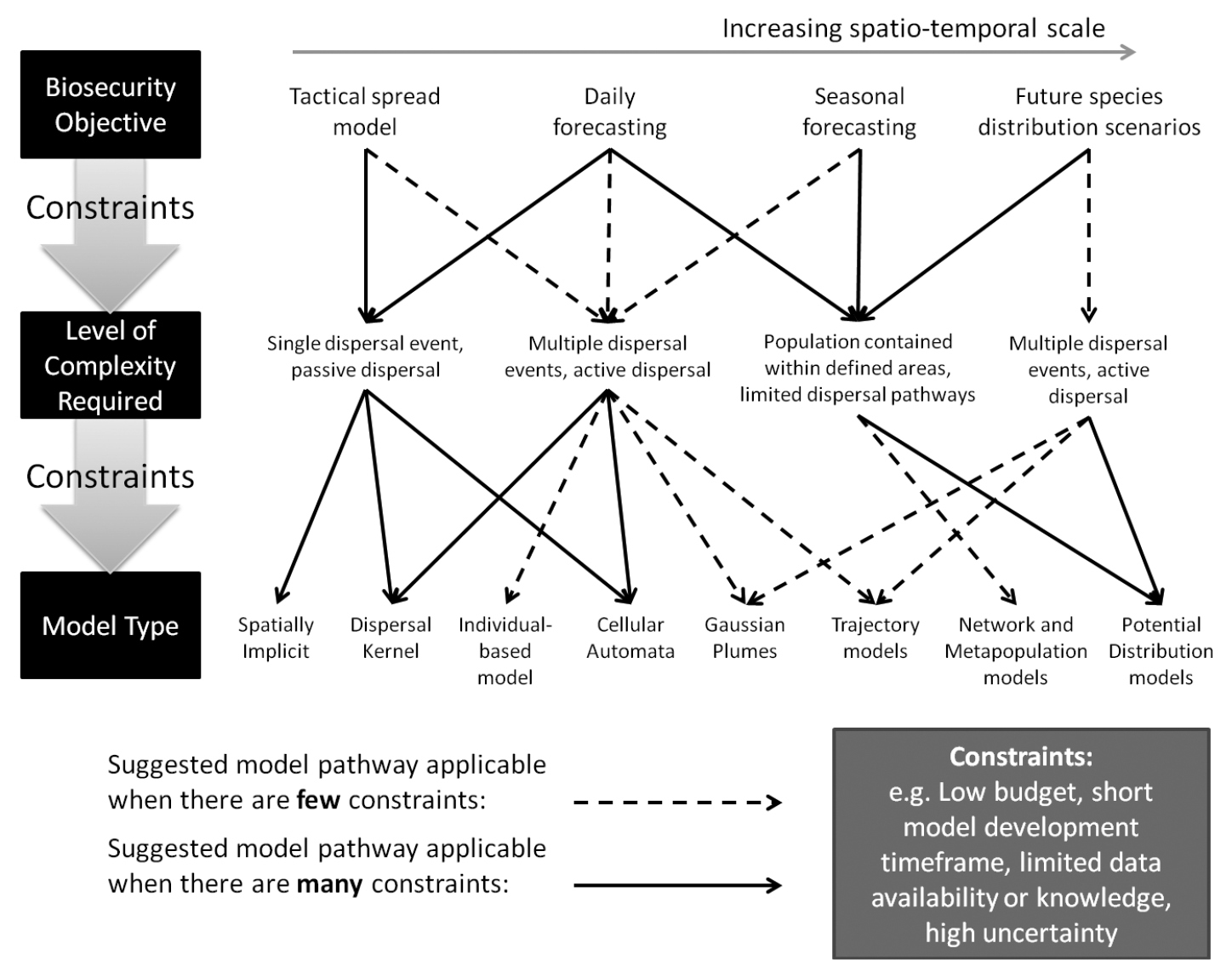
A framework is suggested for post-entry dispersal modelling (Fig. 1). We expand on the key aspects of this framework in the following sections. Important to this process are clearly defined biosecurity objectives and scale informing the conceptual model (1), with an awareness of the constraints (such as time and the value of the problem in terms of pest/pathogen impact). Two primary issues are faced when modelling post-entry spread: obtaining data for model parameterisation and the difficulty of modelling multiple dispersal pathways (
A framework for the model building process, when two data sets are available – one for fitting and one for evaluating the model (after
In the model formulation (2), a consideration of scale and complexity is paramount. How complex can the model be, given the availability of data and knowledge of the system, and how complex does the model need to be to address the salient questions? In general the complexity of a model is determined by the model scope and purpose, and the complexity of the study system. However, in rapid response situations, the inevitable lack of data means that in general it is best to construct simple (perhaps over-simplified) models rather than complex models (
As more data becomes available, model complexity and specificity can be increased. When selecting a modelling method, we suggest that modellers should consider a) the minimum level of model complexity required to address the pressing and foreseeable management and research questions, and b) the maximum level of model complexity that can be supported by the available knowledge and resources. Where a < b, the modeller has the option of choosing to build an elaborate model, perhaps capable of addressing unthought-of questions. Where a > b there is an information deficit and decision-makers expectations and confidence in the model results may need to be managed carefully. For pre-border risk assessments, there is latent demand for spatially-explicit spread models that are combined with impacts. Unfortunately, the initialisation of such models is a critically sensitive factor. Prior to an incursion and establishment of a pest or pathogen, the starting point for the spread model is unknown, and unknowable, a situation similar to that of the state of Schrödinger’s Cat prior to opening the box.
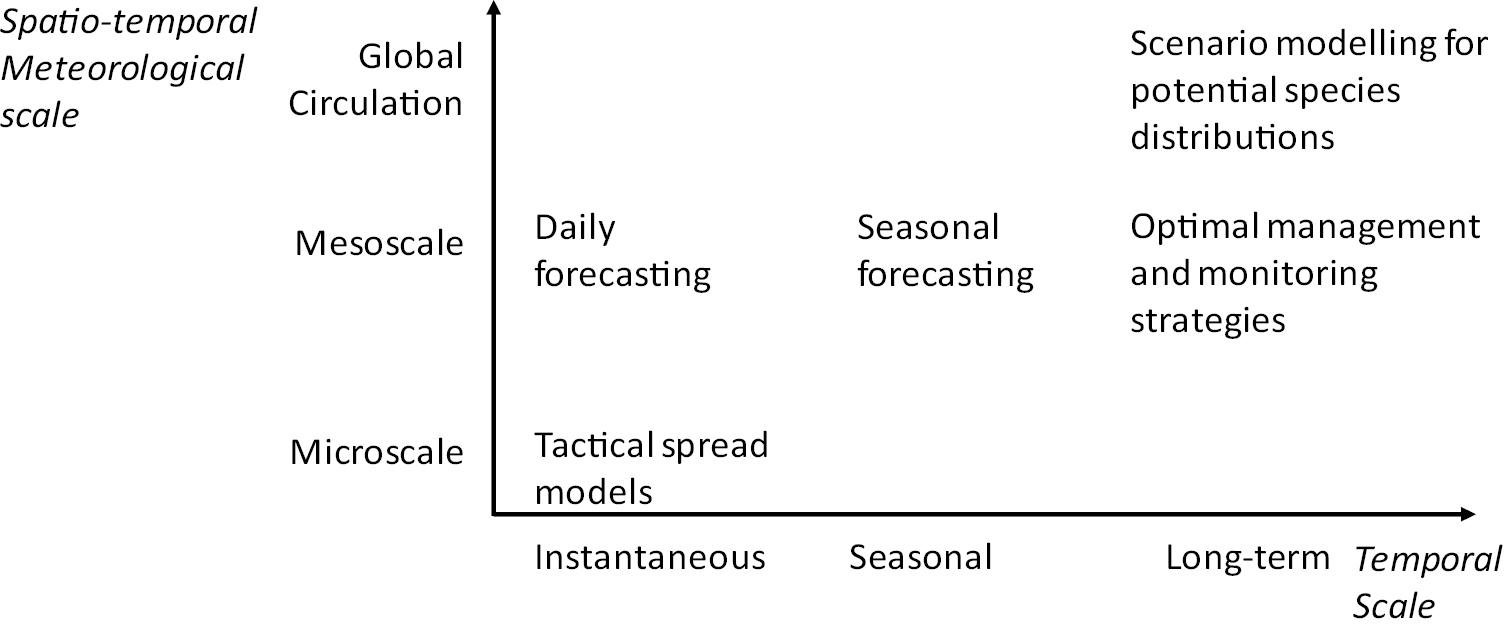
Temporal and spatial scale has an important role in the modelling process. Models for invasion post-entry pest spread most often need to be spatially-explicit, as landscape structure can impact on the invasion process significantly (
Although operating at different spatio-temporal scales, all of these models are likely to be required as soon as possible in a biological invasion. For example, long-term pest risk assessments are critical to help evaluate the suitable level of response to the incursion, e.g. through an economic analysis (e.g.
Pest and pathogen modelling foci at different spatio-temporal scales.
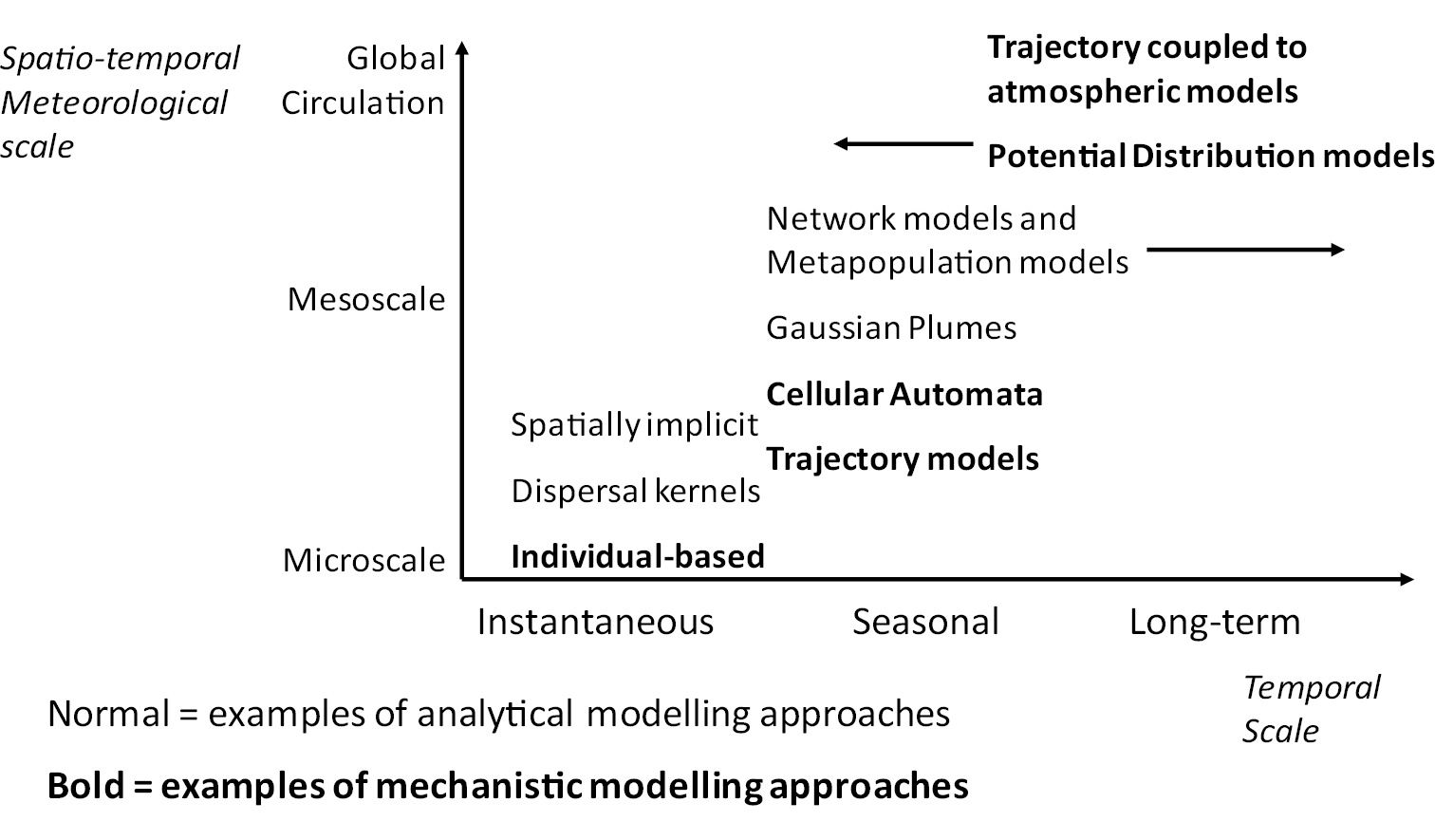
To summarise the broad range of methods that are available to modellers, we have identified important attributes of each of the model types that are commonly used to simulate post-entry spread (Table 1). For each of these methods, we highlight the common model focus and application, with references to some key examples in the literature. We identify the common data requirements, and highlight the overall advantages and disadvantages of each method. We also categorise the models according to their most appropriate temporal and spatial scale of use (although we acknowledge there is some potential overlap between our categories and that our references may refer to more than one scale or approach).
Summary of model types and characteristics commonly used in post-entry pest and pathogen modelling, including examples and key references.
| Model Type | Spatially implicit | Dispersal Kernels | Individual-based models | Cellular Automata | Gaussian Plumes | Trajectory models | Network models and Metapopulation models | Potential distribution models |
|---|---|---|---|---|---|---|---|---|
| Common model focus (see also Fig. 2) | Tactical spread | Tactical spread; Daily forecasting | Tactical spread; Daily forecasting | Seasonal forecasting | Tactical spread; Daily forecasting | Seasonal forecasting; Scenario modelling for future distributions | Seasonal forecasting; Scenario modelling for future distributions | Potential distribution, identifying the assets at risk, providing a forcing function for the rate of spread across heterogeneous landscapes, Scenario modelling for future distributions |
| Common model spatial scale (micro, meso, global circulation) | Mesoscale | Microscale; Mesoscale | Microscale; Mesoscale | Mesoscale | Mesoscale; Global circulation | Mesoscale; Global circulation | Mesoscale; Global circulation | Mesoscale; Global circulation |
| Common model temporal scale (instantaneous, seasonal, long-term) |
Seasonal; long-term | Instantaneous | Instantaneous; Seasonal | Seasonal | Seasonal; long-term | Seasonal; long-term | Seasonal; long-term | long-term |
| Category (analytical or mechanistic) | Analytical | Analytical | Mechanistic | Mechanistic | Analytical | Mechanistic | Analytical | Analytical (majority), but some can be mechanistic or semi-mechanistic. |
| General pest /pathogen characteristics | Passive movement; Single dispersal event | Passive movement; Single dispersal event | Any mobile organism | Any mobile organism | Passive movement; Single dispersal event | Any mobile organism | Population contained within a clearly identifiable area/habitat. Specialists. | Any organism. Works best with sessile organisms, though some models can accommodate mobile organisms. |
| Common data requirements | Pest source; Dispersal rate; Population density | Population density; Dispersal distance; Dispersal rate; Wind speed and direction; Pest source. | Individual life-history; Behavioural rules (including dispersal); Pest source; Landscape data (e.g. land use, habitat suitability etc). | Dispersal distance; Dispersal rate; Wind speed and direction; Pest source; Pest population dynamics; Landscape data (e.g. land use, habitat suitability etc). | Pest source; Wind speed and direction; Dispersal rate; Population density | Pest source; Multi-level wind field data; Elevation; Pest dispersal ecology and survival; | Habitat patches; Population dynamics; Population density; Dispersal rate (between patches); ‘connectivity’ and ‘travel cost’ between patches. | Well known pest distribution at least in native range (presence and absence) and ideally some information on introduced range; constraints on pest survival and population growth |
| Invasion ecology examples | ||||||||
| Key References | ||||||||
| Advantage | Minimal data requirements. | Minimal data requirements. | Accounts for environmental heterogeneity; Emergence; Flexibility; Scale free. | Accounts for environmental heterogeneity; Less computationally and data intensive than fully individual-based models. | An analytical simplification of atmospheric complexity; minimal data requirements. | Incorporates atmospheric or oceanic processes; Can account for landscape effects (e.g. roughness, elevation); | Relatively simple; Allows examination of important processes including connectivity and flow at multiple scales. | Long-term risks; incorporates environmental change; large scale. |
| Disadvantage | Highly simplistic; assumes uniform landscape; May not be biologically realistic. | Often assumes uniform landscape; Relatively simplistic treatment of dispersal; May not be biologically realistic. | Complexity; data intensive; Species specific | data intensive; Strong influence of grid cell size and shape on dispersal; Relatively simplistic treatment of dispersal. | Assumes uniform landscape; | Complexity; data intensive | Assumes clearly defined habitat patches; complete knowledge of ‘empty’ and ‘occupied’ sites; Relatively simplistic treatment of dispersal. | Ignores evolutionary change; Scale specific. |
By understanding the scale at which policy questions are formulated (Fig. 2), we can align the spatio-temporal scale at which particular modelling techniques are best applied (Fig. 3) to identify which modelling methods may be best to use for particular policy questions (Table 1). However, it should be noted that in many cases it is necessary to examine an incursion event at multiple spatial and temporal scales and there can be significant advantages in doing so, such as an increased understanding of the invasion process and accounting for non-equilibrium of the species with the environment (
Examples of dispersal modelling techniques employed at different spatio-temporal scales.
Flow diagram to illustrate the modelling process with concepts from this paper.
To explore the flow diagram, first consider the objective of the modelling exercise, the spatial temporal scale and consider the existing knowledge about the organism (as indicated above); this defines the level of model complexity (with constraints). For example, if the objective is to make a tactical spread model very quickly, about an organism that little is known about, then this means there are many constraints on the approach that can be taken (i.e. time and knowledge). Due to this constraint, the level of complexity is best viewed as a single dispersal event with passive dispersal (i.e. solid line, Fig. 4). At this level of complexity, the options available in this case (Spatially Implicit, Dispersal Kernel or Cellular Automata, Fig. 4) are suitable even under many constraints (solid line, Fig. 4), so any of these could be applied, with the final decision based on the appropriate spatio-temporal scale and to some extent the personal preference of the modeller (arrow at top, Fig. 4).
To give a more complex example, the objective is to make a large-scale seasonal pest forecast model about an organism that has multiple modes of dispersal, both active and passive ranging across multiple habitats/pathways. As this objective relates to a complex model including multiple dispersal events and active dispersal, then a model of this complexity is only possible to construct if there are few constraints (i.e. dash line). The model development requires a certain level of existing knowledge about the organism’s behaviour and perhaps a certain financial budget or amount of time to gather the information and develop the model. Given that the constraints are surmountable and it is possible to acquire the knowledge within the timeframe, then different model types might be chosen, again relating to further constraints on model complexity/development such as budget/time: (1) if there are many constraints at this point the suggestion is the use of dispersal kernels or cellular automata – which simplify the known complexity of the dispersal events and mechanisms, or (2) if there are few constraints then a mechanistic approach may be taken such as individual-based modelling, gaussian plumes or trajectory models, all of which can better represent the complexity of the dispersal mechanisms. The other option for seasonal pest forecasting, if the first constraint cannot be met (i.e. the modeller is required to assume highly simplified behaviour such as limited dispersal pathways within defined areas), then the modeller can make the assumption of a more limited mode of dispersal that allows for such constraints. This leads to a different approach where the preferred option (if there are further constraints relating to e.g. model development time and budget) would be potential distribution models; however if a more dynamic approach is feasible by fewer constraints at this point (e.g. as there is good data availability about movement pathways) then network models/metapopulation models may be more appropriate.
The importance of integrating field-based research and surveillance efforts with models as part of an ongoing multidisciplinary research effort continues to be highlighted in the literature (
Dispersal data are amongst the most difficult to collect and interpret. Post-hoc inferential methods relying on date-stamped geographical location records for invasions may be biased, incomplete and collected at a scale that is poorly suited for spread modelling (
Observations of the movement of an individual may have little informative value for the spread of a population. Spread rates for a species may vary greatly in relation to the potential movement of individuals, depending upon the suitability of the environment for population establishment and growth (
A key data requirement common for many models is to identify the incursion source. This underlines the importance of studies and models to identify entry points. However, even this may not be readily identifiable, and modellers must often work with partial information on an already spreading population without knowing the precise origin. Next, information on dispersal, such as movement rates, distances and directions are required. In more mechanistic methods, population dynamics and life-history parameters are required in order to simulate how individual dispersal events arise from a population. Habitat suitability and landscape data are also highly important in mechanistic, spatially-explicit simulations. A mechanistic method allows us to include important landscape interactions, such as foraging for food and breeding hosts, which can be critical factors of spread. This is one of the major advantages of a mechanistic method over an analytical one, as we are rarely able to adequately use an analytical approach to include the interaction of the organism with the landscape.
Ongoing monitoring and data acquisition is one solution to providing modelling support for decision-making in the face of knowledge scarcity. Existing models may be updated by calibration to fit new data as it is acquired, for example using methods such as a Kalman filter (most commonly used to update state-space equation model estimations with newly observed values, e.g.
Knowledge gaps may relate to either a gap in knowledge of how a process is understood and therefore modelled (i.e. model uncertainty), or the uncertainty with which we can estimate the true value of a model parameter (parametric uncertainty). If the knowledge of a critical process is incomplete, it is prudent to be cautious, and to be wary of management imperatives derived from regression-based patterns. The method of multiple competing hypotheses (
Parameter uncertainty, as a knowledge gap, is a function of data paucity and the availability of statistical methods. Model complexity also contributes to parameter uncertainty. On the one hand, highly complex models may contain so many parameters that not all may be known adequately, but on the other hand models that are very simple often contain parameters that are hard to estimate. Commonly, individual parameters are estimated through monitoring or experimental data targeted towards those parameters. These parameter estimates are then used in the model. If uncertainty in the estimates is quantified then the parameter uncertainty can be fed through the model to provide an estimate of parameter sensitivity. Other sources of uncertainty can also be incorporated into models through developing Bayesian posterior confidence intervals, such as measurement error or errors assigned to ad hoc parameter values (
- garnering parameter values from analyses of the existing literature; or
- minimising some measure of discrepancy between model output and the limited set of observations available, and which includes Approximate Bayesian Computation (ABC;
Marjoram et al. 2003 ) and the inverse model problem.
Simulation is perhaps the best way to assign ‘prediction’ error or intervals to deterministic models, given uncertain starting conditions of the pest/pathogen population. Posterior prediction intervals can also be derived for stochastic models through cross-validation, and more generally through the use of independent test and training data sets. Generating prediction intervals to be tested against new data sets also falls under the rubric of model validation (e.g.
Common to all dynamic models is a temporal limit in quantifying model error. In this case an error is associated with a single time step, and in iteratively running a model then the error is compounded. The consequence of this compounding error is that long term utility of any dispersal model is dogged by severe and growing uncertainty. Two options are then available: (i) continual updating of results by resetting the model’s initial conditions to the current conditions (e.g., the Kalman Filter process); or (ii) applying a decision method developed for severe uncertainty. Continual updating is consistent with both A3MF and Bayesian model updating, or ‘learning’: as new data arrive then our understanding of the processes, our ability to predict system processes, or belief in our model should also improve. However, continual updating requires ongoing monitoring to feed the model any change in system state as it occurs. Continual updating is most appropriate for developing tactical management responses to invasions, but does nothing to address the inability of these models to address strategic questions in a timely manner.
In contrast, decision making under severe uncertainty is common for long-term strategy development, or where continual updating is a cost-prohibitive option. Several analytical decision frameworks have been developed for dealing with severe uncertainty, with the two most popular being robust optimisation (RO) (
There is no single recipe for constructing a model of post-entry spread, due the diversity of policy applications, ecological and landscape contexts, temporal and spatial scales and possible techniques to employ. We have attempted to present some practical guidelines on how to approach model framing and construction for post-entry spread in invasion ecology by identifying what method may be most suitable to apply to particular policy questions, at what spatial and temporal scale, given the available data and knowledge. In recent years, we have seen the evolution of more process-based, mechanistic models that attempt to capture system dynamics and complexity. This trend has been supported (and perhaps encouraged) by the availability of suitable computer platforms capable of processing the immense amount of information required to simulate these processes, as well as the availability of suitable covariate data.
The need for a more rapid response in outbreak situations has resulted in the recent development of fine-scale dispersal models designed to forecast and backcast spread for surveillance and response activities (
However, even when armed with limitless computing power and knowledge of a species’ dispersal ecology we cannot forecast far into the future with high precision. We should be wary therefore of applying increasingly sophisticated mechanistic models and running them for long-term forecasts; the results may appear to have a fine resolution, but this should not be confused with reality – in such instances an analytical approach may be preferable, where fewer variables, constrained behaviour and obvious lack of precision make more explicit the model uncertainties and inaccuracies. Overall, there is great value in combining modelling methods; indeed it is likely to be necessary as the multi-dimensionality of the problem of post-entry pest spread will often require an integrated, multi-model, multi-scale approach, aligned with an empirical surveillance programme.
The most pressing limitations to applying spread modelling to post-entry invasion ecology are clearly not methodological. Modellers are spoilt for choice. The biggest constraints concern our knowledge of the rates of spread of organisms in novel landscapes at fine spatial and temporal scales, as well as across the time course of invasions. A clear challenge here is the cost of monitoring the spread of invasive organisms, which typically sees a rapid decline in interest once an organism stops being an eradication target. Options for overcoming this problem include placing more emphasis on the collection of time-stamped location data for invasive species, “crowd-sourcing” initiatives, and the development of a rich library of spread rate data for different organisms.
This work was primarily completed during the course of a post-doctoral fellowship at CSIRO, supported by the Cooperative Research Centre for Plant Biosecurity. The authors would like to thank the International Pest Risk Modelling Workgroup http://www.pestrisk.org/ for their support and helpful discussions that have led to the development of this article.